Adding big numbers

One of the most frequently asked interview questions: How do you add arbitrarily large number? Or a variation of that: Add nodes of two singly linked lists, producing a third list. Let's progressively look into how to do this more efficiently moving away from the interview problem.

For example,

72345678898723456754489234667744553453453469 +
50965245089245673459076671243800945678976232

This number doesn't fit in any commercially available CPU registers, in fact, these numbers are larger than what can fit in a 128 bit word. The maximum number that can fit in a 128-bit register is `340282366920938463463374607431768211455`! But many of the scientific and astronomical calculations will need to operate on these kind of very large numbers. There are libraries to deal with this, like the GMP library ([GNU MP Bignum Library](https://gmplib.org/)). But lets not get into it for now, we will try to figure out how to do this without any library support.

We will start with the excercise/interview question, how to add two singly linked lists.

Input

Pointer to two lists of single digits

Output

Pointer to a new list where each node is a digit of the summed value of two nodes from each of the input nodes.

There are a couple of things that we should keep in mind

• The lists need not be of equal length

• Remember to propagate the carry to the first node (most significant digit)

The most easiest (and buggy) approach is to walk through the list, extract the numbers, add it up and construct a list from it.

  struct list *add_list(struct list *l1, struct list *l2)
  {
          unsigned long long num1 = 0, num2 = 0;

          while (l1) {
                  num1 = num1 * 10 + l1->data;
                  l1 = l1->next;
          }

          while (l2) {
                  num2 = num2 * 10 + l2->data;
                  l2 = l2->next;
          }

          num3 = num1 + num2;

          return construct_list(num3);
  }

It's easy to figure out why this code is buggy; even if the two numbers extracted from the lists are smaller than 8 bytes (word size of a typical computer), the sum can overflow, resulting in a wrong answer.

Since the numbers can be of different sizes and there can be a carry from the next digit (this is important because we cannot go back to the previous digit if there is a carry and want to add it back, remember this is a singly linked list), two lists cannot be added from the beginning. How did we do it in our school?

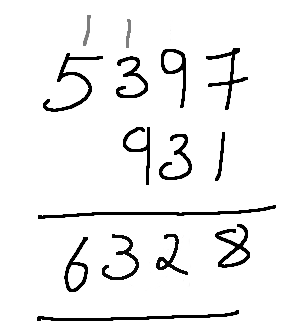
It's obvious that the addition will have to be done from right to left, but that is not possible since it is a singly linked list. What can be done is, reverse both the list, do the addition and add the resulting digits to a new list.

  struct node *add_list(struct node *l1, struct node *l2)
  {
          struct node *rl1, *rl2, *l3 = NULL;
          unsigned carry = 0;

          rl1 = reverse_list(l1);
          rl2 = reverse_list(l2);

          while (rl1 || rl2) {
                  unsigned d1 = rl1 ? rl1->data : 0,
                           d2 = rl2 ? rl2->data : 0,
                           d = d1 + d2;

                  d += carry;
                  carry = 0;

                  if (d >= 10) {
                          carry = 1;
                          d = d % 10;
                  }

                  append_node(&l3, d);

                  rl1 = rl1 ? rl1->next : NULL;
                  rl2 = rl2 ? rl2->next : NULL;
          }

          if (carry)
                  append_node(&l3, 1);

          return l3;
  }

This same logic can extended to add numbers which are represented as a string.

The reverse function by itself is an interview question. But that is easily done with rearrangement of pointers.

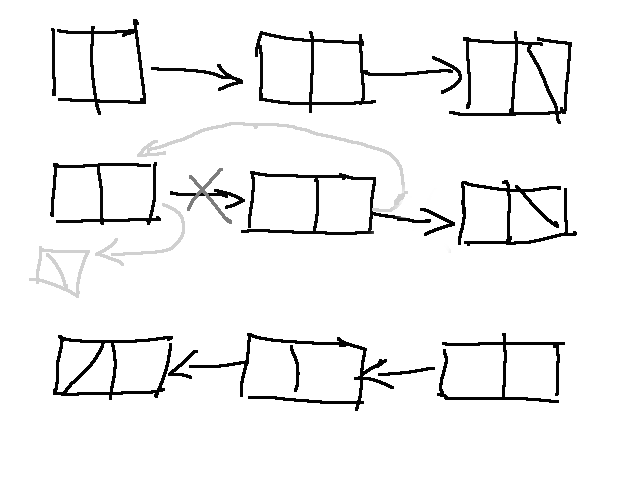
The list reversing can be understood easily if we take only two nodes, make the first node point to `NULL` and the second node point to the first.

  /* we need a pointer to hold the next node, so as its not lost */
  struct list *next = head->next;
  head->next = NULL;
  next->next = head;

From here all we need to do is extend to three nodes. Since the first node is already reversed, we will move head to point to the next, and repeat the same operation.

  struct node *reverse_list(struct node *head)
  {
          struct node *next, *prev = NULL;

          while (head) {
                  next = head->next;
                  head->next = prev;
                  prev = head;
                  head = next;
          }
          return prev;
  }

This time we just used another pointer `prev` to keep track of the previous node, instead of just assigning a `NULL`.

Coming back to the big number addition, though that was an elegant (??) solution, it is sub-optimal. If it was a interview question we could just leave it here.

Computers can do calculations on large numbers (64 bits or 128 bits) in one single operation. Also the list holds one digit per node; even a short int is a big waste of space for a single digit (4-bits are enough). The data size can be reduced further using a char data type. Or we could just use the entire `unsigned long long` data type (or whatever type the data is), so that we will use less space and don't have to do digit by digit operation.

Now that we have moved from the interview exercise problem, let's not stick with singly linked list. Doubly linked list is a more efficient data structure for this problem (Arrays are better, to avoid some memory allocation complexities, which we will see later we will stick with doubly linked lists for now). Moreover we can move back to play with the carry. Here is how we can do it.

• Start from the right most entry (end of the list) and add the new number

• if the number overflows, place only the overflowed amount in the entry, and add one to the previous node (or create one if one doesn't exist).

To save memory , we can start with one element list and add a node as we continue to overflow. We will look into this is a future post.